Video

Final Report

Please check out our final report documenting our work and results!

ESE 350 - Tunable Analog Hearing Aid - Final Report

Test results

We ran some test using resistor values from the optimiser and got several frequency response charts from it.

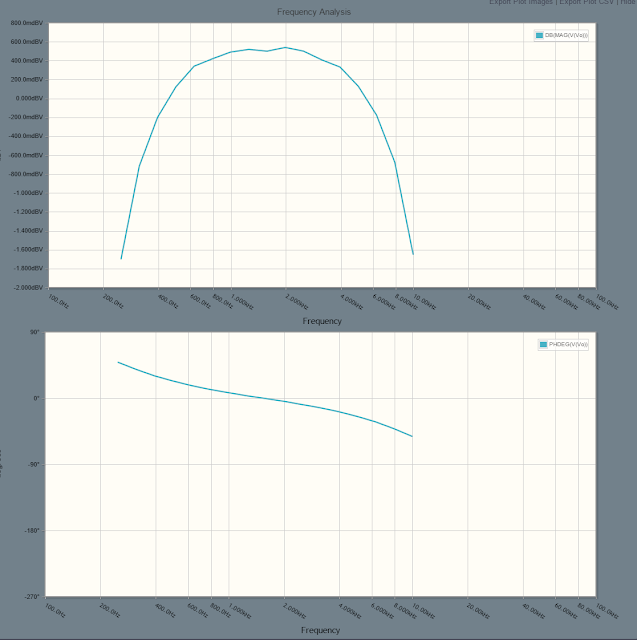
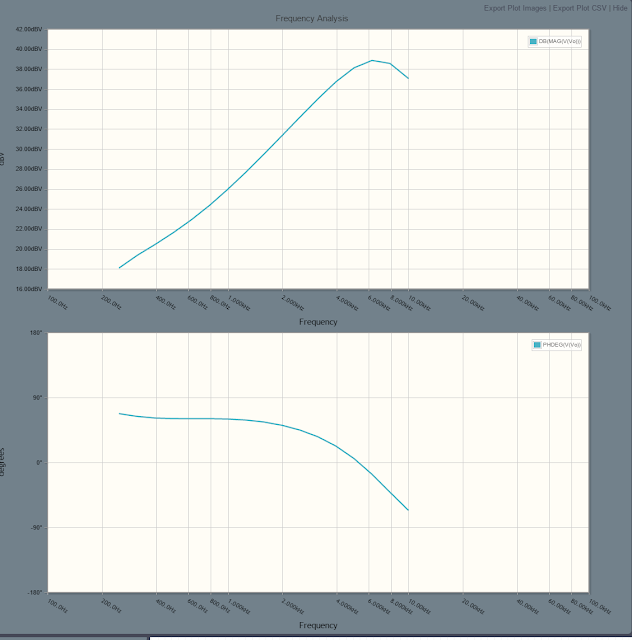
This is the result through a single filter. The yellow is the input and the blue is the output. The size is expected because we use the summing amplifer to do most of the amplification. In addition we were expecting the output to grow at higher frequencies given the input to the optimizer.

This is the result through the pass-through filter. This as well is what we expected - simple reduction is amplitude so when it goes through the summing amplifier it is the correct magnitude.

This is where things get interesting. This is the final outpu from the summing amplifer. We would expect this to be a simple sum of the two magnitudes. However, unlike the first output, it is actually smaller at higher frequencies.

We currently think that the problem has to do with phase. If we look at the phase of the bandpass filters we are using: 

We can see that the phase is -90 degrees for most of the bandwidth and then gets worse as we near the peak. When two waves are 180 degress out of phase, they cancel perfectly. This is clearly a problem we did not anticipate and are not accounting for in the optimization. We are currently looking into solutions involving phase shift circuitry or different ways of optimizing the values.

Implementation

For implementation we decided to start small with only two bandpass filters. This is easy because we are using LM358 opamp chips which each have two op-amps per chip. Each filter requires 3 resistors as well as a gain potentiometer. For this reason, we got MCP4261 chips. These are variable potentiometers with two potentiometers per IC. This lets us create a full filter with only two resistor chips and half of an op-amp chip. We also decided to add the unmodified input to the summing amplifier. This lets us set a gain across the spectrum in the case that the user has general hearing loss across all frequencies.

In the center, there are five ICs. Four of them are the MCP4261. Under the crossed yellow wires is the LM358 chip. These five ICs make up the two bandpass filters we have so far. Beneath them on the same column is another MCP4261, this chip is used to set the gain on the pass-through data. On the bottom left, there is a summing amplifer that takes the three voltages from the filters and pass-through and creates a final output.

On the left is an mbed. We use this to program the MCP4261s over SPI. 

MATLAB Optimization Results

Before testing our MATLAB optimization on audiograms, we validated the individual parts of the algorithm, including the bandpass filter function we created and the method of combining frequency response graphs against circuit simulations in CircuitLab. After this validation process, we tested the entire script on audiogram samples. 

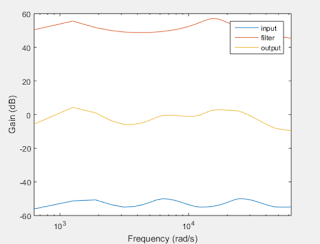
The following figures show the optimization script's ability to compensate for various types of hearing loss, including sensineural, conductive, and mixed. In all of these cases, the algorithm performs well and is able to bring the output hearing to a normal range of -20 dB - 10. However, for the mixed hearing loss, there is a small dip below -20 dB at roughly 15000 rad/s. This indicates that we may need an additional bandpass filter in the higher frequency regions or higher gain capabilities. 

Figure 1: Sensineural Audiogram

Figure 2: Conducitve Audiogram

Figure 3: Mixed Audiogram

Figure 4: Low Pass filter representation of audiogram

Figure 4 above is a low pass filter representation of a hearing impaired person's audiogram. This result will be used for testing and validation of the optimization in our circuit.

Prototype 1 - Functional Block Diagrams

We have completed prototype 1. This prototype consists of a circuit containing 2 programmable bandpass filters and programmable gains for each filter and the original sound wave. A final programmable gain is also included. The functional block diagram is shown in Figure 1. Details of the implementation of this circuit will be posted soon.

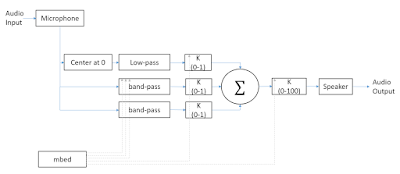Figure 1: Functional Block Diagram of circuit for prototype 1 

In order to determine the optimal filter and gain values for the circuit in Figure 1, we created a MATLAB script that performed frequency response analysis of our circuit and utilized a non linear least squared optimizer. A functional block diagram of the optimization script is shown in Figure 2.

Figure 2: Functional Block Diagram

The cost function used for the non linear optimization combines the frequency response magnitude curves of each of the parallel band pass filters and the original sound signal. The optimal function y = 0 represents an ideal frequency response, which is a decibel gain of 0. This signifies no deviation in amplitude from the original sound.

The non linear optimization function, in this case the MATLAB function lsqnonlin, attempts to minimize the difference between the ideal function and the filter circuit by varying the desired parameters of the filter resistors and gains. The function then outputs the variables found by the optimization.


The band pass filters were modeled using the following transfer function model for an MFB bandpass filter:

Each resistor value, R1, R2, and R3, was varied during the optimization.

We ran several simulations of filter designs during prototyping. We very quickly came to the general idea of using several bandpass filters to handle various bands of frequency separately and then combine the outputs together using a summing amplifier. It took us another week to settle on the filter design and parameters as well as the number of filters. We eventually settled on 6 1st order bandpass filters with center frequencies evenly spaced out between 250Hz and 10000Hz. This gave us the following design.

If we modify the resistor values of each filter we have total control over center frequency, gain and quality factor, though the "standard" values shown give a smooth, neutral amplification:

If the user needs amplification at high frequencies we can modify the gain resistors to get the following response:

We also studied the possibility of chaining the filters by passing the output of one to the input of another. This would give us a higher roll-off rate and could be used by adding some switching circuitry. The use case of this would be a user with a significant amount of hearing loss in certain bandwidths and no hearing loss in others. In this case, we would not want to overamplify the bandwidth in which their hearing is not impaired.

An example response is like this: 

Here, the roll-off rate is twice that of the previous filter and has useful amplification only in the requested areas. 

Hearing Profiles

Hearing profiles, or audiograms, vary from person to person. The audiogram specifies the minimum amplitude of sound an invididual is able to hear. For example, in Figure 1, the blue line delineates what the minimum amplitude of the sound at the specified frequency the individual is able to hear. In this case, the individual's needs a sound at 4000 Hz to be a minimum of 60 dB to be hear, which is very poor. The ideal range for minimum dB level is above 20 dB across all frequencies.

The goal of our hearing aid is to be tunable to accomodate these various audiograms. The following is an example of a common type of audiogram for a hearing impaired person. 

Figure 2: Sensorineural Hearing Loss

In Figure 1, you will see an example of sensorineural hearing loss, which is the most common type of hearing loss. 90% of hearing impaired people have this type of hearing loss in which there is damage to the inner ear. 

Figure 2: Conductive Hearing Loss

Figure 2 is an example of conductive hearing loss in which the outer or middle ear are not properly working. This causes a block. 

Figure 3: Mixed Hearing Loss

Figure 3 is an example of mixed hearing loss. Expectedly, this is a mix of both conductive and sensorineural hearing loss. 

Our ideal tunable hearing aid system would attempt to amplify the frequencies for which the individual requires a larger minimum amplitude. In particular, a set of selectively tuned band pass filters would amplify the frequency ranges in which the individual has poor hearing. This set of band pass filters will be tuned by modifying programmable resistor values within each bandpass filter circuit. In particular, the band pass filters can be modified for a different corner frequency, quality factor (or width), and amplitude. 

Based on the above, we may want to focus more on improving the hearing aid performance for sensorineural hearing profiles, since the vast majority of hearing impaired people suffer from this type of hearing loss. Sensorineural hearing may require also having the ability to increase decrease the attenuation of the filter and having a large amplitude, which may require using higher order band pass filters. 

Project Proposal

Project Title: Tunable Analog Hearing Aid

Team Members: Golam Kibria, Alex Perry

Motivation: Current hearing aid solutions amplify all frequencies of sound. However, hearing frequency profiles vary depending on the user. A programmable hearing aid solution would allow the user to customize the hearing aid to their preferences and needs. Additionally, it would allow the user to modify the hearing aid as the user’s hearing abilities change, for example, due to aging.

Goals:

1. Design a hearing aid that can be modified by the user to amplify a certain set of frequency ranges
2. Allow the user to program the hearing aid through a simple mechanism, such as USB
3. Create a microcontroller based interface for the user to input the frequency ranges they desire to amplify and the magnitude of amplification
4. Create a gui that displays the characteristics of the amplifier, allows the user to modify the parameters, and generate code to enact the change

Methodology

1. Research hearing profiles of those who use hearing aid to determine number of variable bandpass filters required to get the necessary distribution
2. Research various types of bandpass filters to determine ideal types for this application
1. Power consumption
2. Signal quality
3. Number of components
4. Configurability using digital potentiometers
3. Use circuit simulations to compare potential circuits (CircuitLab frequency analysis)
4. breadboard chosen circuit for real world testing
5. Prototype programming software to take user input, compute necessary variable parameters, and program hearing aid

Testing and Evaluation

Circuit simulation

• We will simulate potential circuits in CircuitLab to characterize performance and determine the most ideal circuits

Physical Prototype

• We will create a breadboard prototype to determine real world performance of the chosen circuit. We will test the signal outputs through an oscilloscope and the audio quality of the output

Project Components

Hardware

Band pass filters(capacitors, op amps, programmable potentiometers, resistors)

Summing Amplifier circuit

Microphone

Speaker

Mbed for programming circuit elements.

Software

Python GUI to allow user to specify (frequency range and?) amount of amplification

Microcontroller software to take gui input over USB and translate into a series of I2C or SPI commands to send to programmable circuit elements

Deliverables

Baseline:

Breadboard prototype using programmable components

Basic software to generate I2C or SPI messages

Reach:

PCB with low power components

GUI to program various components

Timeline

By 4/8	Perform research on hearing profiles and bandpass filters Create circuit simulation to test various band pass filters
4/9-4/15	Finish simulation testing and breadboard circuit with fixed components Order programmable parts
4/16-4/22	Breadboard circuit with programmable circuits. Build simple UI to program components. Design PCB
4/23-4/28	DEMO DAY - Finalize initial prototype
4/29-5/6	Assemble PCB Program GUI for interfacing with circuit.
5/10	Hand in report and github.